This module includes several search algorithms, which are customizable to arbitrary purposes. It is mostly a wrapper around the Visitor interface of the Boost Graph Library, and the respective search functions.
| bfs_search | Breadth-first traversal of a directed or undirected graph. |
| dfs_search | Depth-first traversal of a directed or undirected graph. |
| dijkstra_search | Dijsktra traversal of a directed or undirected graph, with non-negative weights. |
| bellman_ford_search | Bellman-Ford traversal of a directed or undirected graph, with negative weights. |
| astar_search | Heuristic \(A^*\) search on a weighted, directed or undirected graph for the case where all edge weights are non-negative. |
| BFSVisitor | A visitor object that is invoked at the event-points inside the bfs_search() algorithm. |
| DFSVisitor | A visitor object that is invoked at the event-points inside the dfs_search() algorithm. |
| DijkstraVisitor | A visitor object that is invoked at the event-points inside the dijkstra_search() algorithm. |
| BellmanFordVisitor | A visitor object that is invoked at the event-points inside the bellman_ford_search() algorithm. |
| AStarVisitor | A visitor object that is invoked at the event-points inside the astar_search() algorithm. |
| StopSearch | If this exception is raised from inside any search visitor object, the search is aborted. |
In this module, most documentation examples will make use of the network search_example.xml, shown below.
>>> gt.seed_rng(42)
>>> g = gt.load_graph("search_example.xml")
>>> name = g.vertex_properties["name"]
>>> weight = g.edge_properties["weight"]
>>> pos = gt.graph_draw(g, vertex_text=name, vertex_font_size=12, vertex_shape="double_circle",
... vertex_fill_color="#729fcf", vertex_pen_width=3,
... edge_pen_width=weight, output="search_example.pdf")
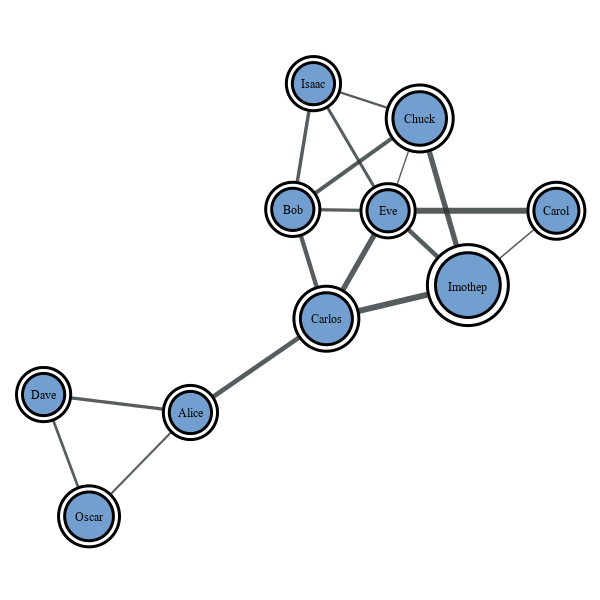
This is the network used in the examples below. The width of the edges correspond to the values of the “weight” property map.
A visitor object that is invoked at the event-points inside the bfs_search() algorithm. By default, it performs no action, and should be used as a base class in order to be useful.
This is invoked on every vertex of the graph before the start of the graph search.
This is invoked when a vertex is encountered for the first time.
This is invoked on a vertex as it is popped from the queue. This happens immediately before examine_edge() is invoked on each of the out-edges of vertex u.
This is invoked on every out-edge of each vertex after it is discovered.
This is invoked on each edge as it becomes a member of the edges that form the search tree.
This is invoked on back or cross edges for directed graphs and cross edges for undirected graphs.
This is invoked on the subset of non-tree edges whose target vertex is colored gray at the time of examination. The color gray indicates that the vertex is currently in the queue.
This is invoked on the subset of non-tree edges whose target vertex is colored black at the time of examination. The color black indicates that the vertex has been removed from the queue.
This invoked on a vertex after all of its out edges have been added to the search tree and all of the adjacent vertices have been discovered (but before the out-edges of the adjacent vertices have been examined).
Breadth-first traversal of a directed or undirected graph.
| Parameters : | g : Graph
source : Vertex
visitor : BFSVisitor (optional, default: BFSVisitor())
|
|---|
See also
Notes
A breadth-first traversal visits vertices that are closer to the source before visiting vertices that are further away. In this context “distance” is defined as the number of edges in the shortest path from the source vertex.
The time complexity is \(O(V + E)\).
The pseudo-code for the BFS algorithm is listed below, with the annotated event points, for which the given visitor object will be called with the appropriate method.
BFS(G, source)
for each vertex u in V[G] initialize vertex u
color[u] := WHITE
d[u] := infinity
end for
color[source] := GRAY
d[source] := 0
ENQUEUE(Q, source) discover vertex source
while (Q != Ø)
u := DEQUEUE(Q) examine vertex u
for each vertex v in Adj[u] examine edge (u,v)
if (color[v] = WHITE) (u,v) is a tree edge
color[v] := GRAY
ENQUEUE(Q, v) discover vertex v
else (u,v) is a non-tree edge
if (color[v] = GRAY)
... (u,v) has a gray target
else
... (u,v) has a black target
end for
color[u] := BLACK finish vertex u
end while
References
| [bfs] | Edward Moore, “The shortest path through a maze”, International Symposium on the Theory of Switching, 1959 |
| [bfs-bgl] | http://www.boost.org/doc/libs/release/libs/graph/doc/breadth_first_search.html |
| [bfs-wikipedia] | http://en.wikipedia.org/wiki/Breadth-first_search |
Examples
We must define what should be done during the search by subclassing BFSVisitor, and specializing the appropriate methods. In the following we will keep track of the distance from the root, and the predecessor tree.
class VisitorExample(gt.BFSVisitor):
def __init__(self, name, pred, dist):
self.name = name
self.pred = pred
self.dist = dist
def discover_vertex(self, u):
print("-->", self.name[u], "has been discovered!")
def examine_vertex(self, u):
print(self.name[u], "has been examined...")
def tree_edge(self, e):
self.pred[e.target()] = int(e.source())
self.dist[e.target()] = self.dist[e.source()] + 1
With the above class defined, we can perform the BFS search as follows.
>>> dist = g.new_vertex_property("int")
>>> pred = g.new_vertex_property("int")
>>> gt.bfs_search(g, g.vertex(0), VisitorExample(name, pred, dist))
--> Bob has been discovered!
Bob has been examined...
--> Eve has been discovered!
--> Chuck has been discovered!
--> Carlos has been discovered!
--> Isaac has been discovered!
Eve has been examined...
--> Imothep has been discovered!
--> Carol has been discovered!
Chuck has been examined...
Carlos has been examined...
--> Alice has been discovered!
Isaac has been examined...
Imothep has been examined...
Carol has been examined...
Alice has been examined...
--> Oscar has been discovered!
--> Dave has been discovered!
Oscar has been examined...
Dave has been examined...
>>> print(dist.a)
[0 2 2 1 1 3 1 1 3 2]
>>> print(pred.a)
[0 3 6 0 0 1 0 0 1 6]
A visitor object that is invoked at the event-points inside the dfs_search() algorithm. By default, it performs no action, and should be used as a base class in order to be useful.
This is invoked on every vertex of the graph before the start of the graph search.
This is invoked on the source vertex once before the start of the search.
This is invoked when a vertex is encountered for the first time.
This is invoked on every out-edge of each vertex after it is discovered.
This is invoked on each edge as it becomes a member of the edges that form the search tree.
This is invoked on the back edges in the graph. For an undirected graph there is some ambiguity between tree edges and back edges since the edge (u,v) and (v,u) are the same edge, but both the tree_edge() and back_edge() functions will be invoked. One way to resolve this ambiguity is to record the tree edges, and then disregard the back-edges that are already marked as tree edges. An easy way to record tree edges is to record predecessors at the tree_edge event point.
This is invoked on forward or cross edges in the graph. In an undirected graph this method is never called.
This is invoked on vertex u after finish_vertex has been called for all the vertices in the DFS-tree rooted at vertex u. If vertex u is a leaf in the DFS-tree, then the finish_vertex() function is called on u after all the out-edges of u have been examined.
Depth-first traversal of a directed or undirected graph.
| Parameters : | g : Graph
source : Vertex
visitor : DFSVisitor (optional, default: DFSVisitor())
|
|---|
See also
Notes
When possible, a depth-first traversal chooses a vertex adjacent to the current vertex to visit next. If all adjacent vertices have already been discovered, or there are no adjacent vertices, then the algorithm backtracks to the last vertex that had undiscovered neighbors. Once all reachable vertices have been visited, the algorithm selects from any remaining undiscovered vertices and continues the traversal. The algorithm finishes when all vertices have been visited.
The time complexity is \(O(V + E)\).
The pseudo-code for the DFS algorithm is listed below, with the annotated event points, for which the given visitor object will be called with the appropriate method.
DFS(G)
for each vertex u in V
color[u] := WHITE initialize vertex u
end for
time := 0
call DFS-VISIT(G, source) start vertex s
DFS-VISIT(G, u)
color[u] := GRAY discover vertex u
for each v in Adj[u] examine edge (u,v)
if (color[v] = WHITE) (u,v) is a tree edge
call DFS-VISIT(G, v)
else if (color[v] = GRAY) (u,v) is a back edge
...
else if (color[v] = BLACK) (u,v) is a cross or forward edge
...
end for
color[u] := BLACK finish vertex u
References
| [dfs-bgl] | http://www.boost.org/doc/libs/release/libs/graph/doc/depth_first_search.html |
| [dfs-wikipedia] | http://en.wikipedia.org/wiki/Depth-first_search |
Examples
We must define what should be done during the search by subclassing DFSVisitor, and specializing the appropriate methods. In the following we will keep track of the discover time, and the predecessor tree.
class VisitorExample(gt.DFSVisitor):
def __init__(self, name, pred, time):
self.name = name
self.pred = pred
self.time = time
self.last_time = 0
def discover_vertex(self, u):
print("-->", self.name[u], "has been discovered!")
self.time[u] = self.last_time
self.last_time += 1
def examine_edge(self, e):
print("edge (%s, %s) has been examined..." % \
(self.name[e.source()], self.name[e.target()]))
def tree_edge(self, e):
self.pred[e.target()] = int(e.source())
With the above class defined, we can perform the DFS search as follows.
>>> time = g.new_vertex_property("int")
>>> pred = g.new_vertex_property("int")
>>> gt.dfs_search(g, g.vertex(0), VisitorExample(name, pred, time))
--> Bob has been discovered!
edge (Bob, Eve) has been examined...
--> Eve has been discovered!
edge (Eve, Isaac) has been examined...
--> Isaac has been discovered!
edge (Isaac, Bob) has been examined...
edge (Isaac, Chuck) has been examined...
--> Chuck has been discovered!
edge (Chuck, Eve) has been examined...
edge (Chuck, Isaac) has been examined...
edge (Chuck, Imothep) has been examined...
--> Imothep has been discovered!
edge (Imothep, Carol) has been examined...
--> Carol has been discovered!
edge (Carol, Eve) has been examined...
edge (Carol, Imothep) has been examined...
edge (Imothep, Carlos) has been examined...
--> Carlos has been discovered!
edge (Carlos, Eve) has been examined...
edge (Carlos, Imothep) has been examined...
edge (Carlos, Bob) has been examined...
edge (Carlos, Alice) has been examined...
--> Alice has been discovered!
edge (Alice, Oscar) has been examined...
--> Oscar has been discovered!
edge (Oscar, Alice) has been examined...
edge (Oscar, Dave) has been examined...
--> Dave has been discovered!
edge (Dave, Oscar) has been examined...
edge (Dave, Alice) has been examined...
edge (Alice, Dave) has been examined...
edge (Alice, Carlos) has been examined...
edge (Imothep, Chuck) has been examined...
edge (Imothep, Eve) has been examined...
edge (Chuck, Bob) has been examined...
edge (Isaac, Eve) has been examined...
edge (Eve, Imothep) has been examined...
edge (Eve, Bob) has been examined...
edge (Eve, Carol) has been examined...
edge (Eve, Carlos) has been examined...
edge (Eve, Chuck) has been examined...
edge (Bob, Chuck) has been examined...
edge (Bob, Carlos) has been examined...
edge (Bob, Isaac) has been examined...
>>> print(time.a)
[0 7 5 6 3 9 1 2 8 4]
>>> print(pred.a)
[0 3 9 9 7 8 0 6 1 4]
A visitor object that is invoked at the event-points inside the dijkstra_search() algorithm. By default, it performs no action, and should be used as a base class in order to be useful.
This is invoked on every vertex of the graph before the start of the graph search.
This is invoked on a vertex as it is popped from the queue. This happens immediately before examine_edge() is invoked on each of the out-edges of vertex u.
This is invoked on every out-edge of each vertex after it is discovered.
This is invoked when a vertex is encountered for the first time.
Upon examination, if the following condition holds then the edge is relaxed (its distance is reduced), and this method is invoked.
(u, v) = tuple(e)
assert(compare(combine(d[u], weight[e]), d[v]))
Upon examination, if the edge is not relaxed (see edge_relaxed()) then this method is invoked.
This invoked on a vertex after all of its out edges have been added to the search tree and all of the adjacent vertices have been discovered (but before their out-edges have been examined).
Dijsktra traversal of a directed or undirected graph, with non-negative weights.
| Parameters : | g : Graph
source : Vertex
weight : PropertyMap
visitor : DijkstraVisitor (optional, default: DijkstraVisitor())
dist_map : PropertyMap (optional, default: None)
pred_map : PropertyMap (optional, default: None)
combine : binary function (optional, default: lambda a, b: a + b)
compare : binary function (optional, default: lambda a, b: a < b)
zero : int or float (optional, default: 0)
infinity : int or float (optional, default: float('inf'))
|
|---|---|
| Returns : | dist_map : PropertyMap
pred_map : PropertyMap
|
See also
Notes
Dijkstra’s algorithm finds all the shortest paths from the source vertex to every other vertex by iteratively “growing” the set of vertices S to which it knows the shortest path. At each step of the algorithm, the next vertex added to S is determined by a priority queue. The queue contains the vertices in V - S prioritized by their distance label, which is the length of the shortest path seen so far for each vertex. The vertex u at the top of the priority queue is then added to S, and each of its out-edges is relaxed: if the distance to u plus the weight of the out-edge (u,v) is less than the distance label for v then the estimated distance for vertex v is reduced. The algorithm then loops back, processing the next vertex at the top of the priority queue. The algorithm finishes when the priority queue is empty.
The time complexity is \(O(V \log V)\).
The pseudo-code for Dijkstra’s algorithm is listed below, with the annotated event points, for which the given visitor object will be called with the appropriate method.
DIJKSTRA(G, source, weight)
for each vertex u in V initialize vertex u
d[u] := infinity
p[u] := u
end for
d[source] := 0
INSERT(Q, source) discover vertex s
while (Q != Ø)
u := EXTRACT-MIN(Q) examine vertex u
for each vertex v in Adj[u] examine edge (u,v)
if (weight[(u,v)] + d[u] < d[v]) edge (u,v) relaxed
d[v] := weight[(u,v)] + d[u]
p[v] := u
DECREASE-KEY(Q, v)
else edge (u,v) not relaxed
...
if (d[v] was originally infinity)
INSERT(Q, v) discover vertex v
end for finish vertex u
end while
return d
References
| [dijkstra] | E. Dijkstra, “A note on two problems in connexion with graphs”, Numerische Mathematik, 1:269-271, 1959. |
| [dijkstra-bgl] | http://www.boost.org/doc/libs/release/libs/graph/doc/dijkstra_shortest_paths_no_color_map.html |
| [dijkstra-wikipedia] | http://en.wikipedia.org/wiki/Dijkstra’s_algorithm |
Examples
We must define what should be done during the search by subclassing DijkstraVisitor, and specializing the appropriate methods. In the following we will keep track of the discover time, and the predecessor tree.
class VisitorExample(gt.DijkstraVisitor):
def __init__(self, name, time):
self.name = name
self.time = time
self.last_time = 0
def discover_vertex(self, u):
print("-->", self.name[u], "has been discovered!")
self.time[u] = self.last_time
self.last_time += 1
def examine_edge(self, e):
print("edge (%s, %s) has been examined..." % \
(self.name[e.source()], self.name[e.target()]))
def edge_relaxed(self, e):
print("edge (%s, %s) has been relaxed..." % \
(self.name[e.source()], self.name[e.target()]))
With the above class defined, we can perform the Dijkstra search as follows.
>>> time = g.new_vertex_property("int")
>>> dist, pred = gt.dijkstra_search(g, g.vertex(0), weight, VisitorExample(name, time))
--> Bob has been discovered!
edge (Bob, Eve) has been examined...
edge (Bob, Eve) has been relaxed...
--> Eve has been discovered!
edge (Bob, Chuck) has been examined...
edge (Bob, Chuck) has been relaxed...
--> Chuck has been discovered!
edge (Bob, Carlos) has been examined...
edge (Bob, Carlos) has been relaxed...
--> Carlos has been discovered!
edge (Bob, Isaac) has been examined...
edge (Bob, Isaac) has been relaxed...
--> Isaac has been discovered!
edge (Eve, Isaac) has been examined...
edge (Eve, Imothep) has been examined...
edge (Eve, Imothep) has been relaxed...
--> Imothep has been discovered!
edge (Eve, Bob) has been examined...
edge (Eve, Carol) has been examined...
edge (Eve, Carol) has been relaxed...
--> Carol has been discovered!
edge (Eve, Carlos) has been examined...
edge (Eve, Chuck) has been examined...
edge (Isaac, Bob) has been examined...
edge (Isaac, Chuck) has been examined...
edge (Isaac, Eve) has been examined...
edge (Chuck, Eve) has been examined...
edge (Chuck, Isaac) has been examined...
edge (Chuck, Imothep) has been examined...
edge (Chuck, Bob) has been examined...
edge (Carlos, Eve) has been examined...
edge (Carlos, Imothep) has been examined...
edge (Carlos, Bob) has been examined...
edge (Carlos, Alice) has been examined...
edge (Carlos, Alice) has been relaxed...
--> Alice has been discovered!
edge (Imothep, Carol) has been examined...
edge (Imothep, Carlos) has been examined...
edge (Imothep, Chuck) has been examined...
edge (Imothep, Eve) has been examined...
edge (Alice, Oscar) has been examined...
edge (Alice, Oscar) has been relaxed...
--> Oscar has been discovered!
edge (Alice, Dave) has been examined...
edge (Alice, Dave) has been relaxed...
--> Dave has been discovered!
edge (Alice, Carlos) has been examined...
edge (Carol, Eve) has been examined...
edge (Carol, Imothep) has been examined...
edge (Oscar, Alice) has been examined...
edge (Oscar, Dave) has been examined...
edge (Dave, Oscar) has been examined...
edge (Dave, Alice) has been examined...
>>> print(time.a)
[0 7 6 3 2 9 1 4 8 5]
>>> print(pred.a)
[0 3 6 0 0 1 0 0 1 6]
>>> print(dist.a)
[ 0. 8.91915887 9.27141329 4.29277116 4.02118246
12.23513866 3.23790211 3.45487436 11.04391549 7.74858396]
A visitor object that is invoked at the event-points inside the bellman_ford_search() algorithm. By default, it performs no action, and should be used as a base class in order to be useful.
This is invoked on every edge in the graph |V| times.
This is invoked when the distance label for the target vertex is decreased. The edge (u,v) that participated in the last relaxation for vertex v is an edge in the shortest paths tree.
This is invoked if the distance label for the target vertex is not decreased.
This is invoked during the second stage of the algorithm, during the test of whether each edge was minimized. If the edge is minimized then this function is invoked.
This is invoked during the second stage of the algorithm, during the test of whether each edge was minimized. If the edge was not minimized, this function is invoked. This happens when there is a negative cycle in the graph.
Bellman-Ford traversal of a directed or undirected graph, with negative weights.
| Parameters : | g : Graph
source : Vertex
weight : PropertyMap
visitor : DijkstraVisitor (optional, default: DijkstraVisitor())
dist_map : PropertyMap (optional, default: None)
pred_map : PropertyMap (optional, default: None)
combine : binary function (optional, default: lambda a, b: a + b)
compare : binary function (optional, default: lambda a, b: a < b)
zero : int or float (optional, default: 0)
infinity : int or float (optional, default: float('inf'))
|
|---|---|
| Returns : | minimized : bool
dist_map : PropertyMap
pred_map : PropertyMap
|
See also
Notes
The Bellman-Ford algorithm [bellman-ford] solves the single-source shortest paths problem for a graph with both positive and negative edge weights. If you only need to solve the shortest paths problem for positive edge weights, dijkstra_search() provides a more efficient alternative. If all the edge weights are all equal, then bfs_search() provides an even more efficient alternative.
The Bellman-Ford algorithm proceeds by looping through all of the edges in the graph, applying the relaxation operation to each edge. In the following pseudo-code, v is a vertex adjacent to u, w maps edges to their weight, and d is a distance map that records the length of the shortest path to each vertex seen so far. p is a predecessor map which records the parent of each vertex, which will ultimately be the parent in the shortest paths tree
RELAX(u, v, w, d, p)
if (w(u,v) + d[u] < d[v])
d[v] := w(u,v) + d[u] relax edge (u,v)
p[v] := u
else
... edge (u,v) is not relaxed
The algorithm repeats this loop |V| times after which it is guaranteed that the distances to each vertex have been reduced to the minimum possible unless there is a negative cycle in the graph. If there is a negative cycle, then there will be edges in the graph that were not properly minimized. That is, there will be edges (u,v) such that w(u,v) + d[u] < d[v]. The algorithm loops over the edges in the graph one final time to check if all the edges were minimized, returning true if they were and returning false otherwise.
BELLMAN-FORD(G)
for each vertex u in V
d[u] := infinity
p[u] := u
end for
for i := 1 to |V|-1
for each edge (u,v) in E examine edge (u,v)
RELAX(u, v, w, d, p)
end for
end for
for each edge (u,v) in E
if (w(u,v) + d[u] < d[v])
return (false, , ) edge (u,v) was not minimized
else
... edge (u,v) was minimized
end for
return (true, p, d)
The time complexity is \(O(V E)\).
References
| [bellman-ford] | (1, 2) R. Bellman, “On a routing problem”, Quarterly of Applied Mathematics, 16(1):87-90, 1958. |
| [bellman-ford-bgl] | http://www.boost.org/doc/libs/release/libs/graph/doc/bellman_ford_shortest.html |
| [bellman-ford-wikipedia] | http://en.wikipedia.org/wiki/Bellman-Ford_algorithm |
Examples
We must define what should be done during the search by subclassing BellmanFordVisitor, and specializing the appropriate methods. In the following we will keep track of the edge minimizations.
class VisitorExample(gt.BellmanFordVisitor):
def __init__(self, name):
self.name = name
def edge_minimized(self, e):
print("edge (%s, %s) has been minimized..." % \
(self.name[e.source()], self.name[e.target()]))
def edge_not_minimized(self, e):
print("edge (%s, %s) has not been minimized..." % \
(self.name[e.source()], self.name[e.target()]))
With the above class defined, we can perform the Bellman-Ford search as follows.
>>> nweight = g.copy_property(weight)
>>> nweight.a[6] *= -1 # include negative weight in edge (Carlos, Alice)
>>> minimized, dist, pred = gt.bellman_ford_search(g, g.vertex(0), nweight, VisitorExample(name))
edge (Bob, Eve) has been minimized...
edge (Bob, Chuck) has been minimized...
edge (Bob, Carlos) has been minimized...
edge (Bob, Isaac) has been minimized...
edge (Alice, Oscar) has been minimized...
edge (Alice, Dave) has been minimized...
edge (Alice, Carlos) has been minimized...
edge (Carol, Eve) has been minimized...
edge (Carol, Imothep) has been minimized...
edge (Carlos, Eve) has been minimized...
edge (Carlos, Imothep) has been minimized...
edge (Chuck, Eve) has been minimized...
edge (Chuck, Isaac) has been minimized...
edge (Chuck, Imothep) has been minimized...
edge (Dave, Oscar) has been minimized...
edge (Eve, Isaac) has been minimized...
edge (Eve, Imothep) has been minimized...
>>> print(minimized)
True
>>> print(pred.a)
[3 3 9 1 6 1 3 6 1 3]
>>> print(dist.a)
[-28.42555934 -37.34471821 -25.20438243 -41.97110592 -35.20316571
-34.02873843 -36.58860946 -33.55645565 -35.2199616 -36.0029274 ]
A visitor object that is invoked at the event-points inside the astar_search() algorithm. By default, it performs no action, and should be used as a base class in order to be useful.
This is invoked on every vertex of the graph before the start of the graph search.
This is invoked on a vertex as it is popped from the queue (i.e. it has the lowest cost on the OPEN list). This happens immediately before examine_edge() is invoked on each of the out-edges of vertex u.
This is invoked on every out-edge of each vertex after it is examined.
This is invoked when a vertex is first discovered and is added to the OPEN list.
Upon examination, if the following condition holds then the edge is relaxed (its distance is reduced), and this method is invoked.
(u, v) = tuple(e)
assert(compare(combine(d[u], weight[e]), d[v]))
Upon examination, if the edge is not relaxed (see edge_relaxed()) then this method is invoked.
This is invoked when a vertex that is on the CLOSED list is “rediscovered” via a more efficient path, and is re-added to the OPEN list.
This is invoked on a vertex when it is added to the CLOSED list, which happens after all of its out edges have been examined.
Heuristic \(A^*\) search on a weighted, directed or undirected graph for the case where all edge weights are non-negative.
| Parameters : | g : Graph
source : Vertex
weight : PropertyMap
visitor : AStarVisitor (optional, default: AStarVisitor())
heuristic : unary function (optional, default: lambda v: 1)
dist_map : PropertyMap (optional, default: None)
pred_map : PropertyMap (optional, default: None)
cost_map : PropertyMap (optional, default: None)
combine : binary function (optional, default: lambda a, b: a + b)
compare : binary function (optional, default: lambda a, b: a < b)
implicit : bool (optional, default: False)
zero : int or float (optional, default: 0)
infinity : int or float (optional, default: float('inf'))
|
|---|---|
| Returns : | dist_map : PropertyMap
|
See also
Notes
The \(A^*\) algorithm is a heuristic graph search algorithm: an \(A^*\) search is “guided” by a heuristic function. A heuristic function \(h(v)\) is one which estimates the cost from a non-goal state (v) in the graph to some goal state, t. Intuitively, \(A^*\) follows paths (through the graph) to the goal that are estimated by the heuristic function to be the best paths. Unlike best-first search, \(A^*\) takes into account the known cost from the start of the search to v; the paths \(A^*\) takes are guided by a function \(f(v) = g(v) + h(v)\), where \(h(v)\) is the heuristic function, and \(g(v)\) (sometimes denoted \(c(s, v)\)) is the known cost from the start to v. Clearly, the efficiency of \(A^*\) is highly dependent on the heuristic function with which it is used.
The time complexity is \(O((E + V) \log V)\).
The pseudo-code for the \(A^*\) algorithm is listed below, with the annotated event points, for which the given visitor object will be called with the appropriate method.
A*(G, source, h)
for each vertex u in V initialize vertex u
d[u] := f[u] := infinity
color[u] := WHITE
end for
color[s] := GRAY
d[s] := 0
f[s] := h(source)
INSERT(Q, source) discover vertex source
while (Q != Ø)
u := EXTRACT-MIN(Q) examine vertex u
for each vertex v in Adj[u] examine edge (u,v)
if (w(u,v) + d[u] < d[v])
d[v] := w(u,v) + d[u] edge (u,v) relaxed
f[v] := d[v] + h(v)
if (color[v] = WHITE)
color[v] := GRAY
INSERT(Q, v) discover vertex v
else if (color[v] = BLACK)
color[v] := GRAY
INSERT(Q, v) reopen vertex v
end if
else
... edge (u,v) not relaxed
end for
color[u] := BLACK finish vertex u
end while
References
| [astar] | Hart, P. E.; Nilsson, N. J.; Raphael, B. “A Formal Basis for the Heuristic Determination of Minimum Cost Paths”. IEEE Transactions on Systems Science and Cybernetics SSC4 4 (2): 100-107, 1968. DOI: 10.1109/TSSC.1968.300136 |
| [astar-bgl] | http://www.boost.org/doc/libs/release/libs/graph/doc/astar_search.html |
| [astar-wikipedia] | http://en.wikipedia.org/wiki/A*_search_algorithm |
Examples
We will use an irregular two-dimensional lattice as an example, where the heuristic function will be based on the euclidean distance to the target.
The heuristic function will be defined as:
def h(v, target, pos):
return sqrt(sum((pos[v].a - pos[target].a) ** 2))
where pos is the vertex position in the plane.
We must define what should be done during the search by subclassing AStarVisitor, and specializing the appropriate methods. In the following we will keep track of the discovered vertices, and which edges were examined, as well as the predecessor tree. We will also abort the search when a given target vertex is found, by raising the StopSearch exception.
class VisitorExample(gt.AStarVisitor):
def __init__(self, touched_v, touched_e, target):
self.touched_v = touched_v
self.touched_e = touched_e
self.target = target
def discover_vertex(self, u):
self.touched_v[u] = True
def examine_edge(self, e):
self.touched_e[e] = True
def edge_relaxed(self, e):
if e.target() == self.target:
raise gt.StopSearch()
With the above class defined, we can perform the \(A^*\) search as follows.
>>> points = random((500, 2)) * 4
>>> points[0] = [-0.01, 0.01]
>>> points[1] = [4.01, 4.01]
>>> g, pos = gt.triangulation(points, type="delaunay")
>>> weight = g.new_edge_property("double") # Edge weights corresponding to
... # Euclidean distances
>>> for e in g.edges():
... weight[e] = sqrt(sum((pos[e.source()].a -
... pos[e.target()].a) ** 2))
>>> touch_v = g.new_vertex_property("bool")
>>> touch_e = g.new_edge_property("bool")
>>> target = g.vertex(1)
>>> dist, pred = gt.astar_search(g, g.vertex(0), weight,
... VisitorExample(touch_v, touch_e, target),
... heuristic=lambda v: h(v, target, pos))
We can now observe the best path found, and how many vertices and edges were visited in the process.
>>> ecolor = g.new_edge_property("string")
>>> ewidth = g.new_edge_property("double")
>>> ewidth.a = 1
>>> for e in g.edges():
... ecolor[e] = "blue" if touch_e[e] else "black"
>>> v = target
>>> while v != g.vertex(0):
... p = g.vertex(pred[v])
... for e in v.out_edges():
... if e.target() == p:
... ecolor[e] = "#a40000"
... ewidth[e] = 3
... v = p
>>> gt.graph_draw(g, pos=pos, output_size=(300, 300), vertex_fill_color=touch_v,
... vcmap=matplotlib.cm.binary, edge_color=ecolor,
... edge_pen_width=ewidth, output="astar-delaunay.pdf")
<...>
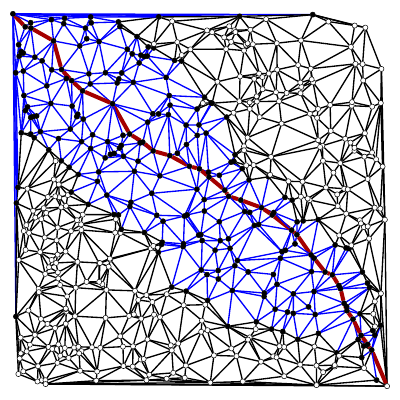
The shortest path is shown in red. The visited edges are shown in blue, and the visited vertices in black.
The \(A^*\) algorithm is very useful for searching implicit graphs, i.e. graphs which are not entirely stored in memory and are generated “on-the-fly” during the search. In the following example we will carry out a search in a hamming hypercube of 10 bits witch has random weights on its edges in the range \([0,1]\). The vertices of the hypercube will be created during the search.
The heuristic function will use the Hamming distance between vertices:
def h(v, target, state):
return sum(abs(state[v].a - target)) / 2
In the following visitor we will keep growing the graph on-the-fly, and abort the search when a given target vertex is found, by raising the StopSearch exception.
from numpy.random import random
class HammingVisitor(gt.AStarVisitor):
def __init__(self, g, target, state, weight, dist, cost):
self.g = g
self.state = state
self.target = target
self.weight = weight
self.dist = dist
self.cost = cost
self.visited = {}
def examine_vertex(self, u):
for i in range(len(self.state[u])):
nstate = list(self.state[u])
nstate[i] ^= 1
if tuple(nstate) in self.visited:
v = self.visited[tuple(nstate)]
else:
v = self.g.add_vertex()
self.visited[tuple(nstate)] = v
self.state[v] = nstate
self.dist[v] = self.cost[v] = float('inf')
for e in u.out_edges():
if e.target() == v:
break
else:
e = self.g.add_edge(u, v)
self.weight[e] = random()
self.visited[tuple(self.state[u])] = u
def edge_relaxed(self, e):
if self.state[e.target()] == self.target:
self.visited[tuple(self.target)] = e.target()
raise gt.StopSearch()
With the above class defined, we can perform the \(A^*\) search as follows.
>>> g = gt.Graph(directed=False)
>>> state = g.new_vertex_property("vector<bool>")
>>> v = g.add_vertex()
>>> state[v] = [0] * 10
>>> target = [1] * 10
>>> weight = g.new_edge_property("double")
>>> dist = g.new_vertex_property("double")
>>> cost = g.new_vertex_property("double")
>>> visitor = HammingVisitor(g, target, state, weight, dist, cost)
>>> dist, pred = gt.astar_search(g, g.vertex(0), weight, visitor, dist_map=dist,
... cost_map=cost, heuristic=lambda v: h(v, array(target), state),
... implicit=True)
We can now observe the best path found, and how many vertices and edges were visited in the process.
>>> ecolor = g.new_edge_property("string")
>>> vcolor = g.new_vertex_property("string")
>>> ewidth = g.new_edge_property("double")
>>> ewidth.a = 1
>>> for e in g.edges():
... ecolor[e] = "black"
>>> for v in g.vertices():
... vcolor[v] = "white"
>>> v = visitor.visited[tuple(target)]
>>> while v != g.vertex(0):
... vcolor[v] = "black"
... p = g.vertex(pred[v])
... for e in v.out_edges():
... if e.target() == p:
... ecolor[e] = "#a40000"
... ewidth[e] = 3
... v = p
>>> vcolor[v] = "black"
>>> pos = gt.graph_draw(g, output_size=(300, 300), vertex_fill_color=vcolor, edge_color=ecolor,
... edge_pen_width=ewidth, output="astar-implicit.pdf")
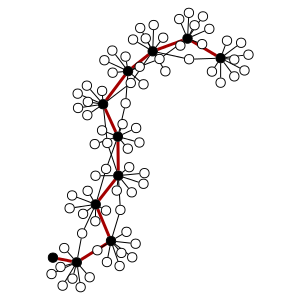
The shortest path is shown in red, and the vertices which belong to it are in black. Note that the number of vertices visited is much smaller than the total number \(2^{10} = 1024\).
If this exception is raised from inside any search visitor object, the search is aborted.