Navigation

graph_tool.topology - Assessing graph topology

Summary

shortest_distance Calculate the distance from a source to a target vertex, or to of all vertices from a given source, or the all pairs shortest paths, if the source is not specified.
shortest_path Return the shortest path from source to target.
pseudo_diameter Compute the pseudo-diameter of the graph.
similarity Return the adjacency similarity between the two graphs.
isomorphism Check whether two graphs are isomorphic.
subgraph_isomorphism Obtain all subgraph isomorphisms of sub in g (or at most max_n subgraphs, if max_n > 0).
mark_subgraph Mark a given subgraph sub on the graph g.
max_cardinality_matching Find a maximum cardinality matching in the graph.
max_independent_vertex_set Find a maximal independent vertex set in the graph.
min_spanning_tree Return the minimum spanning tree of a given graph.
random_spanning_tree Return a random spanning tree of a given graph, which can be directed or undirected.
dominator_tree Return a vertex property map the dominator vertices for each vertex.
topological_sort Return the topological sort of the given graph.
transitive_closure Return the transitive closure graph of g.
tsp_tour Return a traveling salesman tour of the graph, which is guaranteed to be twice as long as the optimal tour in the worst case.
sequential_vertex_coloring Returns a vertex coloring of the graph.
label_components Label the components to which each vertex in the graph belongs.
label_biconnected_components Label the edges of biconnected components, and the vertices which are articulation points.
label_largest_component Label the largest component in the graph.
label_out_component Label the out-component (or simply the component for undirected graphs) of a root vertex.
kcore_decomposition Perform a k-core decomposition of the given graph.
is_bipartite Test if the graph is bipartite.
is_DAG Return True if the graph is a directed acyclic graph (DAG).
is_planar Test if the graph is planar.
make_maximal_planar Add edges to the graph to make it maximally planar.
edge_reciprocity Calculate the edge reciprocity of the graph.

Contents

graph_tool.topology.similarity(g1, g2, label1=None, label2=None, norm=True)

Return the adjacency similarity between the two graphs.

Parameters :

g1 : Graph

First graph to be compared.

g2 : Graph

Second graph to be compared.

label1 : PropertyMap (optional, default: None)

Vertex labels for the first graph to be used in comparison. If not supplied, the vertex indexes are used.

label2 : PropertyMap (optional, default: None)

Vertex labels for the second graph to be used in comparison. If not supplied, the vertex indexes are used.

norm : bool (optional, default: True)

If True, the returned value is normalized by the total number of edges.
Returns :

similarity : float

Adjacency similarity value.

Notes

The adjacency similarity is the sum of equal entries in the adjacency matrix, given a vertex ordering determined by the vertex labels. In other words it counts the number of edges which have the same source and target labels in both graphs.

The algorithm runs with complexity \(O(E_1 + V_1 + E_2 + V_2)\).

Examples

>>> g = gt.random_graph(100, lambda: (3,3))
>>> u = g.copy()
>>> gt.similarity(u, g)
1.0
>>> gt.random_rewire(u)
21
>>> gt.similarity(u, g)
0.03
graph_tool.topology.isomorphism(g1, g2, isomap=False)

Check whether two graphs are isomorphic.

If isomap is True, a vertex PropertyMap with the isomorphism mapping is returned as well.

Examples

>>> g = gt.random_graph(100, lambda: (3,3))
>>> g2 = gt.Graph(g)
>>> gt.isomorphism(g, g2)
True
>>> g.add_edge(g.vertex(0), g.vertex(1))
<...>
>>> gt.isomorphism(g, g2)
False
graph_tool.topology.subgraph_isomorphism(sub, g, max_n=0, random=False)

Obtain all subgraph isomorphisms of sub in g (or at most max_n subgraphs, if max_n > 0).

Parameters :

sub : Graph

Subgraph for which to be searched.

g : Graph

Graph in which the search is performed.

max_n : int (optional, default: 0)

Maximum number of matches to find. If max_n == 0, all matches are found.

random : bool (optional, default: False)

If True, the vertices of g are indexed in random order before the search.
Returns :

vertex_maps : list of PropertyMap objects

List containing vertex property map objects which indicate different isomorphism mappings. The property maps vertices in sub to the corresponding vertex index in g.

edge_maps : list of PropertyMap objects

List containing edge property map objects which indicate different isomorphism mappings. The property maps edges in sub to the corresponding edge index in g.

Notes

The algorithm used is described in [ullmann-algorithm-1976]. It has a worse-case complexity of \(O(N_g^{N_{sub}})\), but for random graphs it typically has a complexity of \(O(N_g^\gamma)\) with \(\gamma\) depending sub-linearly on the size of sub.

References

[ullmann-algorithm-1976](1, 2) Ullmann, J. R., “An algorithm for subgraph isomorphism”, Journal of the ACM 23 (1): 31-42, 1976, DOI: 10.1145/321921.321925
[subgraph-isormophism-wikipedia]http://en.wikipedia.org/wiki/Subgraph_isomorphism_problem

Examples

>>> from numpy.random import poisson
>>> g = gt.random_graph(30, lambda: (poisson(6.1), poisson(6.1)))
>>> sub = gt.random_graph(10, lambda: (poisson(1.9), poisson(1.9)))
>>> vm, em = gt.subgraph_isomorphism(sub, g)
>>> print(len(vm))
35
>>> for i in range(len(vm)):
...   g.set_vertex_filter(None)
...   g.set_edge_filter(None)
...   vmask, emask = gt.mark_subgraph(g, sub, vm[i], em[i])
...   g.set_vertex_filter(vmask)
...   g.set_edge_filter(emask)
...   assert(gt.isomorphism(g, sub))
>>> g.set_vertex_filter(None)
>>> g.set_edge_filter(None)
>>> ewidth = g.copy_property(emask, value_type="double")
>>> ewidth.a += 0.5
>>> ewidth.a *= 2
>>> gt.graph_draw(g, vertex_fill_color=vmask, edge_color=emask,
...               edge_pen_width=ewidth, output_size=(200, 200),
...               output="subgraph-iso-embed.pdf")
<...>
>>> gt.graph_draw(sub, output_size=(200, 200), output="subgraph-iso.pdf")
<...>
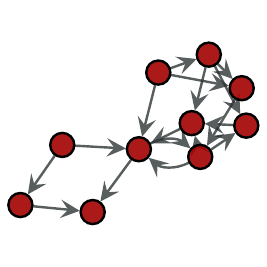
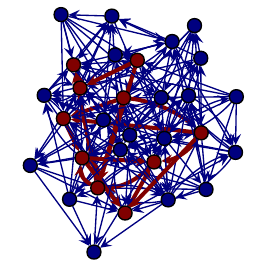
_images/subgraph-iso.png _images/subgraph-iso-embed.png

Left: Subgraph searched, Right: One isomorphic subgraph found in main graph.

graph_tool.topology.mark_subgraph(g, sub, vmap, emap, vmask=None, emask=None)

Mark a given subgraph sub on the graph g.

The mapping must be provided by the vmap and emap parameters, which map vertices/edges of sub to indexes of the corresponding vertices/edges in g.

This returns a vertex and an edge property map, with value type ‘bool’, indicating whether or not a vertex/edge in g corresponds to the subgraph sub.

graph_tool.topology.min_spanning_tree(g, weights=None, root=None, tree_map=None)

Return the minimum spanning tree of a given graph.

Parameters :

g : Graph

Graph to be used.

weights : PropertyMap (optional, default: None)

The edge weights. If provided, the minimum spanning tree will minimize the edge weights.

root : Vertex (optional, default: None)

Root of the minimum spanning tree. If this is provided, Prim’s algorithm is used. Otherwise, Kruskal’s algorithm is used.

tree_map : PropertyMap (optional, default: None)

If provided, the edge tree map will be written in this property map.
Returns :

tree_map : PropertyMap

Edge property map with mark the tree edges: 1 for tree edge, 0 otherwise.

Notes

The algorithm runs with \(O(E\log E)\) complexity, or \(O(E\log V)\) if root is specified.

References

[kruskal-shortest-1956]J. B. Kruskal. “On the shortest spanning subtree of a graph and the traveling salesman problem”, In Proceedings of the American Mathematical Society, volume 7, pages 48-50, 1956. DOI: 10.1090/S0002-9939-1956-0078686-7
[prim-shortest-1957]R. Prim. “Shortest connection networks and some generalizations”, Bell System Technical Journal, 36:1389-1401, 1957.
[boost-mst]http://www.boost.org/libs/graph/doc/graph_theory_review.html#sec:minimum-spanning-tree
[mst-wiki]http://en.wikipedia.org/wiki/Minimum_spanning_tree

Examples

>>> from numpy.random import random
>>> g, pos = gt.triangulation(random((400, 2)) * 10, type="delaunay")
>>> weight = g.new_edge_property("double")
>>> for e in g.edges():
...    weight[e] = linalg.norm(pos[e.target()].a - pos[e.source()].a)
>>> tree = gt.min_spanning_tree(g, weights=weight)
>>> gt.graph_draw(g, pos=pos, output="triang_orig.pdf")
<...>
>>> g.set_edge_filter(tree)
>>> gt.graph_draw(g, pos=pos, output="triang_min_span_tree.pdf")
<...>
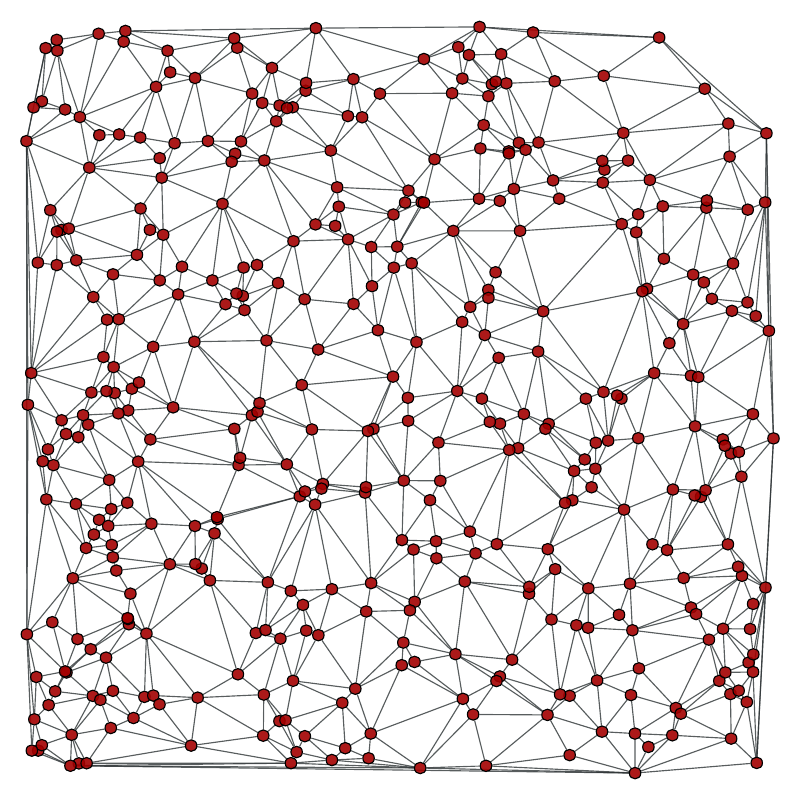
_images/triang_orig.png _images/triang_min_span_tree.png

Left: Original graph, Right: The minimum spanning tree.

graph_tool.topology.random_spanning_tree(g, weights=None, root=None, tree_map=None)

Return a random spanning tree of a given graph, which can be directed or undirected.

Parameters :

g : Graph

Graph to be used.

weights : PropertyMap (optional, default: None)

The edge weights. If provided, the probability of a particular spanning tree being selected is the product of its edge weights.

root : Vertex (optional, default: None)

Root of the spanning tree. If not provided, it will be selected randomly.

tree_map : PropertyMap (optional, default: None)

If provided, the edge tree map will be written in this property map.
Returns :

tree_map : PropertyMap

Edge property map with mark the tree edges: 1 for tree edge, 0 otherwise.

Notes

The typical running time for random graphs is \(O(N\log N)\).

References

[wilson-generating-1996]David Bruce Wilson, “Generating random spanning trees more quickly than the cover time”, Proceedings of the twenty-eighth annual ACM symposium on Theory of computing, Pages 296-303, ACM New York, 1996, DOI: 10.1145/237814.237880
[boost-rst]http://www.boost.org/libs/graph/doc/random_spanning_tree.html

Examples

>>> from numpy.random import random
>>> g, pos = gt.triangulation(random((400, 2)) * 10, type="delaunay")
>>> weight = g.new_edge_property("double")
>>> for e in g.edges():
...    weight[e] = linalg.norm(pos[e.target()].a - pos[e.source()].a)
>>> tree = gt.random_spanning_tree(g, weights=weight)
>>> gt.graph_draw(g, pos=pos, output="rtriang_orig.pdf")
<...>
>>> g.set_edge_filter(tree)
>>> gt.graph_draw(g, pos=pos, output="triang_random_span_tree.pdf")
<...>
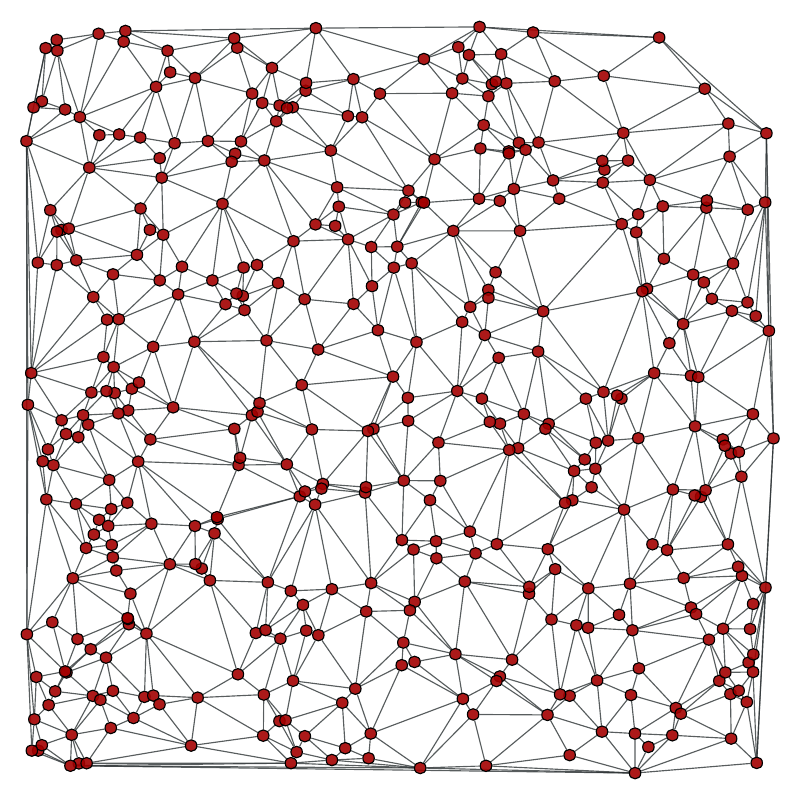
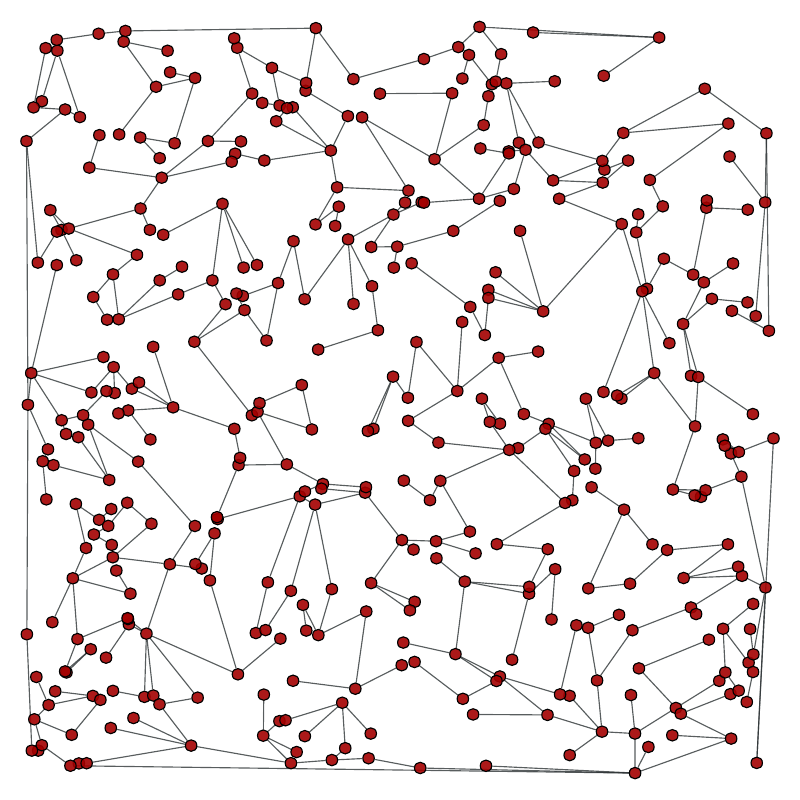
_images/rtriang_orig.png _images/triang_random_span_tree.png

Left: Original graph, Right: A random spanning tree.

graph_tool.topology.dominator_tree(g, root, dom_map=None)

Return a vertex property map the dominator vertices for each vertex.

Parameters :

g : Graph

Graph to be used.

root : Vertex

The root vertex.

dom_map : PropertyMap (optional, default: None)

If provided, the dominator map will be written in this property map.
Returns :

dom_map : PropertyMap

The dominator map. It contains for each vertex, the index of its dominator vertex.

Notes

A vertex u dominates a vertex v, if every path of directed graph from the entry to v must go through u.

The algorithm runs with \(O((V+E)\log (V+E))\) complexity.

References

[dominator-bgl]http://www.boost.org/libs/graph/doc/lengauer_tarjan_dominator.htm

Examples

>>> g = gt.random_graph(100, lambda: (2, 2))
>>> tree = gt.min_spanning_tree(g)
>>> g.set_edge_filter(tree)
>>> root = [v for v in g.vertices() if v.in_degree() == 0]
>>> dom = gt.dominator_tree(g, root[0])
>>> print(dom.a)
[ 0  0  0  0  0  0 62  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
graph_tool.topology.topological_sort(g)

Return the topological sort of the given graph. It is returned as an array of vertex indexes, in the sort order.

Notes

The topological sort algorithm creates a linear ordering of the vertices such that if edge (u,v) appears in the graph, then v comes before u in the ordering. The graph must be a directed acyclic graph (DAG).

The time complexity is \(O(V + E)\).

References

[topological-boost]http://www.boost.org/libs/graph/doc/topological_sort.html
[topological-wiki]http://en.wikipedia.org/wiki/Topological_sorting

Examples

>>> g = gt.random_graph(30, lambda: (3, 3))
>>> tree = gt.min_spanning_tree(g)
>>> g.set_edge_filter(tree)
>>> sort = gt.topological_sort(g)
>>> print(sort)
[ 1 14  2  7 17  0  3  4  5  6  8  9 22 10 11 12 13 16 23 27 15 18 19 20 21
 24 25 26 28 29]
graph_tool.topology.transitive_closure(g)

Return the transitive closure graph of g.

Notes

The transitive closure of a graph G = (V,E) is a graph G* = (V,E*) such that E* contains an edge (u,v) if and only if G contains a path (of at least one edge) from u to v. The transitive_closure() function transforms the input graph g into the transitive closure graph tc.

The time complexity (worst-case) is \(O(VE)\).

References

[transitive-boost]http://www.boost.org/libs/graph/doc/transitive_closure.html
[transitive-wiki]http://en.wikipedia.org/wiki/Transitive_closure

Examples

>>> g = gt.random_graph(30, lambda: (3, 3))
>>> tc = gt.transitive_closure(g)
graph_tool.topology.label_components(g, vprop=None, directed=None, attractors=False)

Label the components to which each vertex in the graph belongs. If the graph is directed, it finds the strongly connected components.

A property map with the component labels is returned, together with an histogram of component labels.

Parameters :

g : Graph

Graph to be used.

vprop : PropertyMap (optional, default: None)

Vertex property to store the component labels. If none is supplied, one is created.

directed : bool (optional, default: None)

Treat graph as directed or not, independently of its actual directionality.

attractors : bool (optional, default: False)

If True, and the graph is directed, an additional array with Boolean values is returned, specifying if the strongly connected components are attractors or not.
Returns :

comp : PropertyMap

Vertex property map with component labels.

hist : ndarray

Histogram of component labels.

is_attractor : ndarray

A Boolean array specifying if the strongly connected components are attractors or not. This returned only if attractors == True, and the graph is directed.

Notes

The components are arbitrarily labeled from 0 to N-1, where N is the total number of components.

The algorithm runs in \(O(V + E)\) time.

Examples

>>> g = gt.random_graph(100, lambda: (poisson(2), poisson(2)))
>>> comp, hist, is_attractor = gt.label_components(g, attractors=True)
>>> print(comp.a)
[14 15 14 14 14  5 14 14 18 14 14  8 14 14 13 14 14 21 14 14  7 23 10 14 14
 14 24  4 14 14  0 14 14 14 25 14 14  1 14 26 14 19  9 14 14  3 14 14 27 28
 29 14 14  6 14 14 14 30 14 14 20 14  2 14 22 33 34 14 14 14 35 14 14 16 14
 11 36 37 14 14 31 14 14 17 14 14 14 14 14  0 14 38 39 32 14 12 14 40 14 14]
>>> print(hist)
[ 2  1  1  1  1  1  1  1  1  1  1  1  1  1 59  1  1  1  1  1  1  1  1  1  1
  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1]
>>> print(is_attractor)
[ True  True  True False False False  True  True False False False False
  True  True False False False False False False False False  True False
 False False False False False False False False False False False False
 False False False False False]
graph_tool.topology.label_largest_component(g, directed=None)

Label the largest component in the graph. If the graph is directed, then the largest strongly connected component is labelled.

A property map with a boolean label is returned.

Parameters :

g : Graph

Graph to be used.

directed : bool (optional, default:None)

Treat graph as directed or not, independently of its actual directionality.
Returns :

comp : PropertyMap

Boolean vertex property map which labels the largest component.

Notes

The algorithm runs in \(O(V + E)\) time.

Examples

>>> g = gt.random_graph(100, lambda: poisson(1), directed=False)
>>> l = gt.label_largest_component(g)
>>> print(l.a)
[1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0
 0 0 0 0 0 0 0 0 1 0 0 0 1 0 1 1 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0
 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1]
>>> u = gt.GraphView(g, vfilt=l)   # extract the largest component as a graph
>>> print(u.num_vertices())
16
graph_tool.topology.label_out_component(g, root)

Label the out-component (or simply the component for undirected graphs) of a root vertex.

Parameters :

g : Graph

Graph to be used.

root : Vertex

The root vertex.
Returns :

comp : PropertyMap

Boolean vertex property map which labels the out-component.

Notes

The algorithm runs in \(O(V + E)\) time.

Examples

>>> g = gt.random_graph(100, lambda: poisson(2.2), directed=False)
>>> l = gt.label_out_component(g, g.vertex(2))
>>> print(l.a)
[1 1 1 1 0 1 1 1 1 1 1 0 1 1 0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 0
 1 1 0 0 1 1 0 1 1 0 0 1 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 1 0 0 1 0 1 1 1 1 1
 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 1 1 0 0]

The in-component can be obtained by reversing the graph.

>>> l = gt.label_out_component(gt.GraphView(g, reversed=True, directed=True),
...                            g.vertex(1))
>>> print(l.a)
[1 1 1 0 0 1 1 0 1 0 0 0 0 1 0 0 0 1 0 0 1 1 0 0 1 0 1 0 0 0 0 0 0 1 1 0 0
 0 1 0 0 0 1 0 1 1 0 0 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 0 1 1 0 1
 1 0 0 0 0 1 1 0 1 1 0 1 1 1 0 0 1 0 0 0 0 0 1 0 0 0]
graph_tool.topology.label_biconnected_components(g, eprop=None, vprop=None)

Label the edges of biconnected components, and the vertices which are articulation points.

An edge property map with the component labels is returned, together a boolean vertex map marking the articulation points, and an histogram of component labels.

Parameters :

g : Graph

Graph to be used.

eprop : PropertyMap (optional, default: None)

Edge property to label the biconnected components.

vprop : PropertyMap (optional, default: None)

Vertex property to mark the articulation points. If none is supplied, one is created.
Returns :

bicomp : PropertyMap

Edge property map with the biconnected component labels.

articulation : PropertyMap

Boolean vertex property map which has value 1 for each vertex which is an articulation point, and zero otherwise.

nc : int

Number of biconnected components.

Notes

A connected graph is biconnected if the removal of any single vertex (and all edges incident on that vertex) can not disconnect the graph. More generally, the biconnected components of a graph are the maximal subsets of vertices such that the removal of a vertex from a particular component will not disconnect the component. Unlike connected components, vertices may belong to multiple biconnected components: those vertices that belong to more than one biconnected component are called “articulation points” or, equivalently, “cut vertices”. Articulation points are vertices whose removal would increase the number of connected components in the graph. Thus, a graph without articulation points is biconnected. Vertices can be present in multiple biconnected components, but each edge can only be contained in a single biconnected component.

The algorithm runs in \(O(V + E)\) time.

Examples

>>> g = gt.random_graph(100, lambda: poisson(2), directed=False)
>>> comp, art, hist = gt.label_biconnected_components(g)
>>> print(comp.a)
[51 51 51 51 51 51 11 52 51 51 44 42 41 45 49 23 19 51 51 32 38 51 24 37 51
 51 51 10  8 51 20 43 51 51 51 51 51 47 46 51 51 13 14 51 51 51 51 33 30 51
  1 21 51 51 51 35 36  6 51 26 27  7 12  4  3 29 28 51 51 51 31 51 51  0 39
 51 51 51 34 40 51 51  9 17 51 51 18 15 22  2 16 50  5 48 51 51 53 51 51 25]
>>> print(art.a)
[1 0 1 0 0 1 0 0 1 1 0 0 1 1 0 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0 1 0 0 0 1 1 0
 0 1 0 0 1 1 0 1 1 0 0 0 1 1 0 1 1 0 0 0 1 0 0 1 0 1 0 0 1 1 0 0 0 0 0 1 1
 1 0 1 1 0 1 0 1 1 0 0 0 0 1 0 1 0 0 0 1 0 0 0 1 0 0]
>>> print(hist)
[ 1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1
  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1
  1 47  1  1]
graph_tool.topology.kcore_decomposition(g, deg='out', vprop=None)

Perform a k-core decomposition of the given graph.

Parameters :

g : Graph

Graph to be used.

deg : string

Degree to be used for the decomposition. It can be either “in”, “out” or “total”, for in-, out-, or total degree of the vertices.

vprop : PropertyMap (optional, default: None)

Vertex property to store the decomposition. If None is supplied, one is created.
Returns :

kval : PropertyMap

Vertex property map with the k-core decomposition, i.e. a given vertex v belongs to the kval[v]-core.

Notes

The k-core is a maximal set of vertices such that its induced subgraph only contains vertices with degree larger than or equal to k.

This algorithm is described in [batagelk-algorithm] and runs in \(O(V + E)\) time.

References

[k-core]http://en.wikipedia.org/wiki/Degeneracy_%28graph_theory%29
[batagelk-algorithm](1, 2) V. Batagelj, M. Zaversnik, “An O(m) Algorithm for Cores Decomposition of Networks”, 2003, arXiv: cs/0310049

Examples

>>> g = gt.collection.data["netscience"]
>>> g = gt.GraphView(g, vfilt=gt.label_largest_component(g))
>>> kcore = gt.kcore_decomposition(g)
>>> gt.graph_draw(g, pos=g.vp["pos"], vertex_fill_color=kcore, vertex_text=kcore, output="netsci-kcore.pdf")
<...>
_images/netsci-kcore.png

K-core decomposition of a network of network scientists.

graph_tool.topology.shortest_distance(g, source=None, target=None, weights=None, max_dist=None, directed=None, dense=False, dist_map=None, pred_map=False)

Calculate the distance from a source to a target vertex, or to of all vertices from a given source, or the all pairs shortest paths, if the source is not specified.

Parameters :

g : Graph

Graph to be used.

source : Vertex (optional, default: None)

Source vertex of the search. If unspecified, the all pairs shortest distances are computed.

target : Vertex (optional, default: None)

Target vertex of the search. If unspecified, the distance to all vertices from the source will be computed.

weights : PropertyMap (optional, default: None)

The edge weights. If provided, the minimum spanning tree will minimize the edge weights.

max_dist : scalar value (optional, default: None)

If specified, this limits the maximum distance of the vertices searched. This parameter has no effect if source is None.

directed : bool (optional, default:None)

Treat graph as directed or not, independently of its actual directionality.

dense : bool (optional, default: False)

If true, and source is None, the Floyd-Warshall algorithm is used, otherwise the Johnson algorithm is used. If source is not None, this option has no effect.

dist_map : PropertyMap (optional, default: None)

Vertex property to store the distances. If none is supplied, one is created.

pred_map : bool (optional, default: False)

If true, a vertex property map with the predecessors is returned. Ignored if source=None.
Returns :

dist_map : PropertyMap

Vertex property map with the distances from source. If source is ‘None’, it will have a vector value type, with the distances to every vertex.

Notes

If a source is given, the distances are calculated with a breadth-first search (BFS) or Dijkstra’s algorithm [dijkstra], if weights are given. If source is not given, the distances are calculated with Johnson’s algorithm [johnson-apsp]. If dense=True, the Floyd-Warshall algorithm [floyd-warshall-apsp] is used instead.

If source is specified, the algorithm runs in \(O(V + E)\) time, or \(O(V \log V)\) if weights are given. If source is not specified, it runs in \(O(VE\log V)\) time, or \(O(V^3)\) if dense == True.

References

[bfs]Edward Moore, “The shortest path through a maze”, International Symposium on the Theory of Switching (1959), Harvard University Press;
[bfs-boost]http://www.boost.org/libs/graph/doc/breadth_first_search.html
[dijkstra]E. Dijkstra, “A note on two problems in connexion with graphs.” Numerische Mathematik, 1:269-271, 1959.
[dijkstra-boost]http://www.boost.org/libs/graph/doc/dijkstra_shortest_paths.html
[johnson-apsp](1, 2) http://www.boost.org/libs/graph/doc/johnson_all_pairs_shortest.html
[floyd-warshall-apsp](1, 2) http://www.boost.org/libs/graph/doc/floyd_warshall_shortest.html

Examples

>>> from numpy.random import poisson
>>> g = gt.random_graph(100, lambda: (poisson(3), poisson(3)))
>>> dist = gt.shortest_distance(g, source=g.vertex(0))
>>> print(dist.a)
[         0          6          3          6 2147483647 2147483647
          6          5          2          4          5          6
          6          3          7          5          4          4
          3          4          2          4          3          3
          4          4          6          6          4          1
          5          2          4          5          3          5
          6          5          4          5 2147483647          9
          4          4          4          6          3          4
          6          6          3          2          4          4
          5          4          5          8          6          6
          5          5          4          5          6          3
          4          3          5          5 2147483647 2147483647
          5          5          8          3          7          4
          5          2          7          5          2          5
          5          5          7          7          4          3
          6          5          5          4          5          5
          4          4          6          5]

>>> dist = gt.shortest_distance(g)
>>> print(dist[g.vertex(0)].a)
[         0          6          3          6 2147483647 2147483647
          6          5          2          4          5          6
          6          3          7          5          4          4
          3          4          2          4          3          3
          4          4          6          6          4          1
          5          2          4          5          3          5
          6          5          4          5 2147483647          9
          4          4          4          6          3          4
          6          6          3          2          4          4
          5          4          5          8          6          6
          5          5          4          5          6          3
          4          3          5          5 2147483647 2147483647
          5          5          8          3          7          4
          5          2          7          5          2          5
          5          5          7          7          4          3
          6          5          5          4          5          5
          4          4          6          5]
graph_tool.topology.shortest_path(g, source, target, weights=None, pred_map=None)

Return the shortest path from source to target.

Parameters :

g : Graph

Graph to be used.

source : Vertex

Source vertex of the search.

target : Vertex

Target vertex of the search.

weights : PropertyMap (optional, default: None)

The edge weights.

pred_map : PropertyMap (optional, default: None)

Vertex property map with the predecessors in the search tree. If this is provided, the shortest paths are not computed, and are obtained directly from this map.
Returns :

vertex_list : list of Vertex

List of vertices from source to target in the shortest path.

edge_list : list of Edge

List of edges from source to target in the shortest path.

Notes

The paths are computed with a breadth-first search (BFS) or Dijkstra’s algorithm [dijkstra], if weights are given.

The algorithm runs in \(O(V + E)\) time, or \(O(V \log V)\) if weights are given.

References

[bfs]Edward Moore, “The shortest path through a maze”, International Symposium on the Theory of Switching (1959), Harvard University Press
[bfs-boost]http://www.boost.org/libs/graph/doc/breadth_first_search.html
[dijkstra]E. Dijkstra, “A note on two problems in connexion with graphs.” Numerische Mathematik, 1:269-271, 1959.
[dijkstra-boost]http://www.boost.org/libs/graph/doc/dijkstra_shortest_paths.html

Examples

>>> from numpy.random import poisson
>>> g = gt.random_graph(300, lambda: (poisson(4), poisson(4)))
>>> vlist, elist = gt.shortest_path(g, g.vertex(10), g.vertex(11))
>>> print([str(v) for v in vlist])
['10', '131', '184', '265', '223', '11']
>>> print([str(e) for e in elist])
['(10, 131)', '(131, 184)', '(184, 265)', '(265, 223)', '(223, 11)']
graph_tool.topology.pseudo_diameter(g, source=None, weights=None)

Compute the pseudo-diameter of the graph.

Parameters :

g : Graph

Graph to be used.

source : Vertex (optional, default: None)

Source vertex of the search. If not supplied, the first vertex in the graph will be chosen.

weights : PropertyMap (optional, default: None)

The edge weights.
Returns :

pseudo_diameter : int

The pseudo-diameter of the graph.

end_points : pair of Vertex

The two vertices which correspond to the pseudo-diameter found.

Notes

The pseudo-diameter is an approximate graph diameter. It is obtained by starting from a vertex source, and finds a vertex target that is farthest away from source. This process is repeated by treating target as the new starting vertex, and ends when the graph distance no longer increases. A vertex from the last level set that has the smallest degree is chosen as the final starting vertex u, and a traversal is done to see if the graph distance can be increased. This graph distance is taken to be the pseudo-diameter.

The paths are computed with a breadth-first search (BFS) or Dijkstra’s algorithm [dijkstra], if weights are given.

The algorithm runs in \(O(V + E)\) time, or \(O(V \log V)\) if weights are given.

References

[pseudo-diameter]http://en.wikipedia.org/wiki/Distance_%28graph_theory%29

Examples

>>> from numpy.random import poisson
>>> g = gt.random_graph(300, lambda: (poisson(3), poisson(3)))
>>> dist, ends = gt.pseudo_diameter(g)
>>> print(dist)
9.0
>>> print(int(ends[0]), int(ends[1]))
0 140
graph_tool.topology.is_bipartite(g, partition=False)

Test if the graph is bipartite.

Parameters :

g : Graph

Graph to be used.

partition : bool (optional, default: False)

If True, return the two partitions in case the graph is bipartite.
Returns :

is_bipartite : bool

Whether or not the graph is bipartite.

partition : PropertyMap (only if partition=True)

A vertex property map with the graph partitioning (or None) if the graph is not bipartite.

Notes

An undirected graph is bipartite if one can partition its set of vertices into two sets, such that all edges go from one set to the other.

This algorithm runs in \(O(V + E)\) time.

References

[boost-bipartite]http://www.boost.org/libs/graph/doc/is_bipartite.html

Examples

>>> g = gt.lattice([10, 10])
>>> is_bi, part = gt.is_bipartite(g, partition=True)
>>> print(is_bi)
True
>>> gt.graph_draw(g, vertex_fill_color=part, output_size=(300, 300), output="bipartite.pdf")
<...>
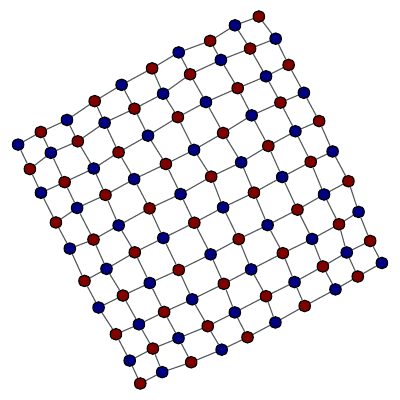
_images/bipartite.png

Bipartition of a 2D lattice.

graph_tool.topology.is_planar(g, embedding=False, kuratowski=False)

Test if the graph is planar.

Parameters :

g : Graph

Graph to be used.

embedding : bool (optional, default: False)

If true, return a mapping from vertices to the clockwise order of out-edges in the planar embedding.

kuratowski : bool (optional, default: False)

If true, the minimal set of edges that form the obstructing Kuratowski subgraph will be returned as a property map, if the graph is not planar.
Returns :

is_planar : bool

Whether or not the graph is planar.

embedding : PropertyMap (only if embedding=True)

A vertex property map with the out-edges indexes in clockwise order in the planar embedding,

kuratowski : PropertyMap (only if kuratowski=True)

An edge property map with the minimal set of edges that form the obstructing Kuratowski subgraph (if the value of kuratowski[e] is 1, the edge belongs to the set)

Notes

A graph is planar if it can be drawn in two-dimensional space without any of its edges crossing. This algorithm performs the Boyer-Myrvold planarity testing [boyer-myrvold]. See [boost-planarity] for more details.

This algorithm runs in \(O(V)\) time.

References

[boyer-myrvold](1, 2) John M. Boyer and Wendy J. Myrvold, “On the Cutting Edge: Simplified O(n) Planarity by Edge Addition” Journal of Graph Algorithms and Applications, 8(2): 241-273, 2004. http://www.emis.ams.org/journals/JGAA/accepted/2004/BoyerMyrvold2004.8.3.pdf
[boost-planarity]http://www.boost.org/libs/graph/doc/boyer_myrvold.html

Examples

>>> from numpy.random import random
>>> g = gt.triangulation(random((100,2)))[0]
>>> p, embed_order = gt.is_planar(g, embedding=True)
>>> print(p)
True
>>> print(list(embed_order[g.vertex(0)]))
[0, 24, 23, 22, 21, 20, 19, 18, 17, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
>>> g = gt.random_graph(100, lambda: 4, directed=False)
>>> p, kur = gt.is_planar(g, kuratowski=True)
>>> print(p)
False
>>> g.set_edge_filter(kur, True)
>>> gt.graph_draw(g, output_size=(300, 300), output="kuratowski.pdf")
<...>
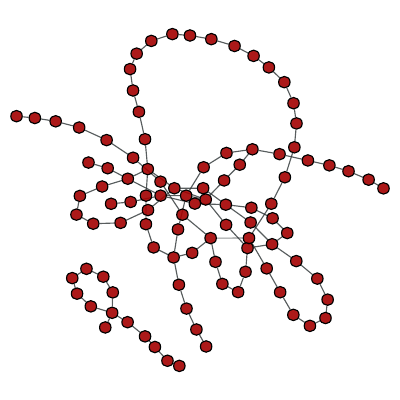
_images/kuratowski.png

Obstructing Kuratowski subgraph of a random graph.

graph_tool.topology.make_maximal_planar(g, unfilter=False)

Add edges to the graph to make it maximally planar.

Parameters :

g : Graph

Graph to be used. It must be a biconnected planar graph with at least 3 vertices.

Notes

A graph is maximal planar if no additional edges can be added to it without creating a non-planar graph. By Euler’s formula, a maximal planar graph with V > 2 vertices always has 3V - 6 edges and 2V - 4 faces.

The input graph to make_maximal_planar() must be a biconnected planar graph with at least 3 vertices.

This algorithm runs in \(O(V + E)\) time.

References

[boost-planarity]http://www.boost.org/libs/graph/doc/make_maximal_planar.html

Examples

>>> g = gt.lattice([42, 42])
>>> gt.make_maximal_planar(g)
>>> gt.is_planar(g)
True
>>> print(g.num_vertices(), g.num_edges())
1764 5286
>>> gt.graph_draw(g, output_size=(300, 300), output="maximal_planar.pdf")
<...>
_images/maximal_planar.png

A maximally planar graph.

graph_tool.topology.is_DAG(g)

Return True if the graph is a directed acyclic graph (DAG).

Notes

The time complexity is \(O(V + E)\).

References

[DAG-wiki]http://en.wikipedia.org/wiki/Directed_acyclic_graph

Examples

>>> g = gt.random_graph(30, lambda: (3, 3))
>>> print(gt.is_DAG(g))
False
>>> tree = gt.min_spanning_tree(g)
>>> g.set_edge_filter(tree)
>>> print(gt.is_DAG(g))
True
graph_tool.topology.max_cardinality_matching(g, heuristic=False, weight=None, minimize=True, match=None)

Find a maximum cardinality matching in the graph.

Parameters :

g : Graph

Graph to be used.

heuristic : bool (optional, default: False)

If true, a random heuristic will be used, which runs in linear time.

weight : PropertyMap (optional, default: None)

If provided, the matching will minimize the edge weights (or maximize if minimize == False). This option has no effect if heuristic == False.

minimize : bool (optional, default: True)

If True, the matching will minimize the weights, otherwise they will be maximized. This option has no effect if heuristic == False.

match : PropertyMap (optional, default: None)

Edge property map where the matching will be specified.
Returns :

match : PropertyMap

Boolean edge property map where the matching is specified.

Notes

A matching is a subset of the edges of a graph such that no two edges share a common vertex. A maximum cardinality matching has maximum size over all matchings in the graph.

If the parameter weight is provided, as well as heuristic == True a matching with maximum cardinality and maximum (or minimum) weight is returned.

If heuristic == True the algorithm does not necessarily return the maximum matching, instead the focus is to run on linear time.

This algorithm runs in time \(O(EV\times\alpha(E,V))\), where \(\alpha(m,n)\) is a slow growing function that is at most 4 for any feasible input. If heuristic == True, the algorithm runs in time \(O(V + E)\).

For a more detailed description, see [boost-max-matching].

References

[boost-max-matching](1, 2) http://www.boost.org/libs/graph/doc/maximum_matching.html
[matching-heuristic]B. Hendrickson and R. Leland. “A Multilevel Algorithm for Partitioning Graphs.” In S. Karin, editor, Proc. Supercomputing ’95, San Diego. ACM Press, New York, 1995, DOI: 10.1145/224170.224228

Examples

>>> g = gt.GraphView(gt.price_network(300), directed=False)
>>> res = gt.max_cardinality_matching(g)
>>> print(res[1])
True
>>> w = res[0].copy("double")
>>> w.a = 2 * w.a + 2
>>> gt.graph_draw(g, edge_color=res[0], edge_pen_width=w, vertex_fill_color="grey",
...               output="max_card_match.pdf")
<...>
_images/max_card_match.png

Edges belonging to the matching are in red.

graph_tool.topology.max_independent_vertex_set(g, high_deg=False, mivs=None)

Find a maximal independent vertex set in the graph.

Parameters :

g : Graph

Graph to be used.

high_deg : bool (optional, default: False)

If True, vertices with high degree will be included first in the set, otherwise they will be included last.

mivs : PropertyMap (optional, default: None)

Vertex property map where the vertex set will be specified.
Returns :

mivs : PropertyMap

Boolean vertex property map where the set is specified.

Notes

A maximal independent vertex set is an independent set such that adding any other vertex to the set forces the set to contain an edge between two vertices of the set.

This implements the algorithm described in [mivs-luby], which runs in time \(O(V + E)\).

References

[mivs-wikipedia]http://en.wikipedia.org/wiki/Independent_set_%28graph_theory%29
[mivs-luby](1, 2) Luby, M., “A simple parallel algorithm for the maximal independent set problem”, Proc. 17th Symposium on Theory of Computing, Association for Computing Machinery, pp. 1-10, (1985) DOI: 10.1145/22145.22146.

Examples

>>> g = gt.GraphView(gt.price_network(300), directed=False)
>>> res = gt.max_independent_vertex_set(g)
>>> gt.graph_draw(g, vertex_fill_color=res, output="mivs.pdf")
<...>
_images/mivs.png

Vertices belonging to the set are in red.

graph_tool.topology.edge_reciprocity(g)

Calculate the edge reciprocity of the graph.

Parameters :

g : Graph

Graph to be used edges.
Returns :

reciprocity : float

The reciprocity value.

Notes

The edge [reciprocity] is defined as \(E^\leftrightarrow/E\), where \(E^\leftrightarrow\) and \(E\) are the number of bidirectional and all edges in the graph, respectively.

The algorithm runs with complexity \(O(E + V)\).

References

[reciprocity](1, 2) S. Wasserman and K. Faust, “Social Network Analysis”. (Cambridge University Press, Cambridge, 1994)
[lopez-reciprocity-2007]Gorka Zamora-López, Vinko Zlatić, Changsong Zhou, Hrvoje Štefančić, and Jürgen Kurths “Reciprocity of networks with degree correlations and arbitrary degree sequences”, Phys. Rev. E 77, 016106 (2008) DOI: 10.1103/PhysRevE.77.016106, arXiv: 0706.3372

Examples

>>> g = gt.Graph()
>>> g.add_vertex(2)
<...>
>>> g.add_edge(g.vertex(0), g.vertex(1))
<Edge object with source '0' and target '1' at 0x33bc710>
>>> gt.edge_reciprocity(g)
0.0
>>> g.add_edge(g.vertex(1), g.vertex(0))
<Edge object with source '1' and target '0' at 0x33bc7a0>
>>> gt.edge_reciprocity(g)
1.0
graph_tool.topology.tsp_tour(g, src, weight=None)

Return a traveling salesman tour of the graph, which is guaranteed to be twice as long as the optimal tour in the worst case.

Parameters :

g : Graph

Graph to be used.

src : Vertex

The source (and target) of the tour.

weight : PropertyMap (optional, default: None)

Edge weights.
Returns :

tour : numpy.ndarray

List of vertex indexes corresponding to the tour.

Notes

The algorithm runs with \(O(E\log V)\) complexity.

References

[tsp-bgl]http://www.boost.org/libs/graph/doc/metric_tsp_approx.html
[tsp]http://en.wikipedia.org/wiki/Travelling_salesman_problem

Examples

>>> g = gt.lattice([10, 10])
>>> tour = gt.tsp_tour(g, g.vertex(0))
>>> print(tour)
[ 0  1  2 11 12 21 22 31 32 41 42 51 52 61 62 71 72 81 82 83 73 63 53 43 33
 23 13  3  4  5  6  7  8  9 19 29 39 49 59 69 79 89 14 24 34 44 54 64 74 84
 91 92 93 94 95 85 75 65 55 45 35 25 15 16 17 18 27 28 37 38 47 48 57 58 67
 68 77 78 87 88 97 98 99 26 36 46 56 66 76 86 96 10 20 30 40 50 60 70 80 90
  0]
graph_tool.topology.sequential_vertex_coloring(g, order=None, color=None)

Returns a vertex coloring of the graph.

Parameters :

g : Graph

Graph to be used.

order : PropertyMap (optional, default: None)

Order with which the vertices will be colored.

color : PropertyMap (optional, default: None)

Integer-valued vertex property map to store the colors.
Returns :

color : PropertyMap

Integer-valued vertex property map with the vertex colors.

Notes

The time complexity is \(O(V(d+k))\), where \(V\) is the number of vertices, \(d\) is the maximum degree of the vertices in the graph, and \(k\) is the number of colors used.

References

[sgc-bgl]http://www.boost.org/libs/graph/doc/sequential_vertex_coloring.html
[graph-coloring]http://en.wikipedia.org/wiki/Graph_coloring

Examples

>>> g = gt.lattice([10, 10])
>>> colors = gt.sequential_vertex_coloring(g)
>>> print(colors.a)
[0 1 0 1 0 1 0 1 0 1 1 0 1 0 1 0 1 0 1 0 0 1 0 1 0 1 0 1 0 1 1 0 1 0 1 0 1
 0 1 0 0 1 0 1 0 1 0 1 0 1 1 0 1 0 1 0 1 0 1 0 0 1 0 1 0 1 0 1 0 1 1 0 1 0
 1 0 1 0 1 0 0 1 0 1 0 1 0 1 0 1 1 0 1 0 1 0 1 0 1 0]

Table Of Contents

Previous topic

graph_tool.stats - Miscellaneous statistics

Next topic

graph_tool.util - Graph utilities

This Page

(Download PDF version)

Latest development version docs are also available.

Navigation

© Copyright 2013, Tiago de Paula Peixoto <tiago@skewed.de>. Last updated on May 21, 2013. Created using Sphinx 1.1.3.